‘Why Do We Have to Learn This?’—Part II
By: Art Bardige

What if, like Leonardo of Pisa, we started from scratch to design a math curriculum for our age? What if we prepare students for business in our time, using the calculating technology of our time, to solve the problems of our time? We already know and have most of the elements and designs at hand.
- We know its technology must be digital and screen-based.
- We know it would require students to be creative because computers will automatically solve most other problems with little human intervention.
- We know it would focus on concepts and real-world problems because they require students to think critically.
- We know it would be visual because images are increasingly becoming our main communication tool and math is in its essence a visual language.
- And we know all students will have to master the use of mathematics for problem-solving because it will be central to their ability to thrive.
Our group began by asking “What if…” questions:
- “What if we reinvented math education for the digital age using spreadsheets?”
- “What if we used the full capability of the web and the power of coding feedback to focus on student learning rather than teacher instructing?”
- “What if we made these lessons, like the other disciplines of STEM, laboratory experiences where students learned by experimentation and not memorization.”
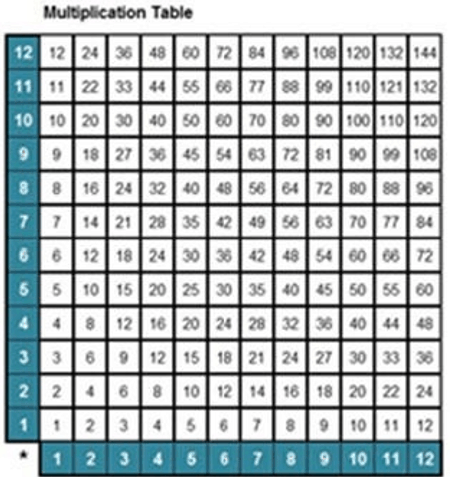
These questions led us to build lessons directly on spreadsheets, imagining lessons as labs. We began by building Labs on conventional math activities like times tables asking students to be creative and to find a way to build them on a spreadsheet in just two steps. We learned to build them up and to the right instead of down because products are then points on a graph. We had them graph functions and construct a triangle with three linear functions. We turned the spreadsheet into a chessboard and asked students to find a power function that would save its inventor. We drew the Empire State Building on a spreadsheet and asked how big a room would be needed to fill a column of pennies that tall. Students worked with data to present the dangers of global warming and decide whether Gordon Moore’s law was right. We built place value machines and decimal calculators to help students visualize these concepts. And we showed them how to build and explore Pascal’s triangle and Fibonnaci’s sequence on a spreadsheet using the simple function of adding two adjacent cells.
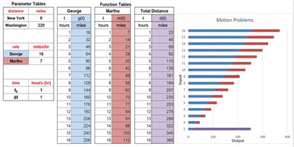
We have found that the ability to easily experiment with design and visualization enabled us to play with concepts, for example, the motion story problems that perplex so many students (e.g. George is riding a fast horse and travels at 16 miles/hour from New York toward Washington and Martha leaves Washington at the same time on a slow carriage at 7 miles/hour. New York is 276 miles from Washington. At what point in the trip will they meet?).
Finding conventional equation representation on even a spreadsheet inadequate, we explored new ways of thinking. We learned to treat problem-solving functionally, building models, with a table for George’s ride, a table for Martha’s ride and in this case a table to sum the distance they covered. We found this functional thinking made standard word problems conceptually simple and easy to understand. We didn’t stop there. We learned to build Parameter tables to give students control over the input variables as a way of achieving closer and closer approximations. In doing so we found commonality we had not before imagined, giving students not only powerful coding techniques (treating key values as variables), but a means to realize and manipulate domains so that they could truly experiment, and think of spreadsheets as actual laboratories and math as an experimental science.
We found that even the most difficult concepts in Leonardo’s math like variable and function became transparent in spreadsheet math and available to much younger kids. We visualize a variable as a table of values, simply a row or column of numbers, concrete and easy to manipulate. We visualize a function as paired columns, one containing input values, the other coded with an = sign to build a rule and thus an output. As students experiment and become familiar with functions, they can learn to use iteration where the output of a function becomes its input, putting input and output in the same column. We found the great power of iteration when we discovered a simple new way to solve quadratic equations replacing the quadratic formula.
We have come to think of math education as problem-solving education based on these characteristics:
- Open-Web: Business today uses the web as its primary resource to work collaboratively, to find information, to use tools, to organize data. If schools are to meet the needs of business in the digital age then like business they have to rely on the web and teach our kids to use this amazing resource for problem solving. Imagine what math would look like if students could use the web with few constraints for all of their work, and yes, for all of their tests including the standardized ones. It may well be that the coming 5G broadband will soon turn schools as well as our cities and towns into open-web sites because the web communication will be much like cell phone communication is today, virtually ubiquitous and not linked to obvious networks.
- Integrated: We live in an increasingly interdisciplinary STEM/STEAM world where science, technology, engineering, art, and yes math are no longer separate disciplines. Imagine preparing students for that world, learning math as real-world problem solving, treated like all of our other laboratory sciences, integrating it with coding, applying it to creative problem-solving processes familiar to engineering, and based on the elements of design and visualization.
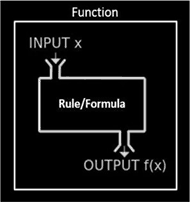
- Functional: Functions, considered by mathematicians as the most important idea in mathematics, were invented four centuries after Leonardo’s work. Represented by the simple picture of a machine that takes an “input” and uses a “rule” to transform it into an output, functions are the building blocks (the atoms) of quantitative models (the molecules) we use to manage data and create the digital world we live in. Imagine preparing students for their future by learning to think and solve problems functionally.
- Creative: Problem solving long considered a crucial skill, often today lost in the mechanical processes, will be reinvented through technology to enable students to be creative, collaborative, critical thinkers to work through real problems and communicate real solutions. Imagine such creative problem-based-learning, now the standard for innovative graduate school education as a standard for K-12 as well.
- Spreadsheets: Having replaced paper and abacuses as the calculating technology in business, spreadsheets must do the same in schools. Spreadsheets are function machines and are used to build business models of all kinds. More than a calculating tool, they enable us to manipulate huge quantities of real-world data and represent data and models visually. Imagine using this ubiquitous, free to schools, shareable, collaborative, highly visual tool to prepare students for the work most will do.
- Coding: Spreadsheets are natural coding platforms. Coding is compelling. The immediate feedback inherent in coding energizes, excites, and provides a powerful tool to drive learning. Imagine students coding on spreadsheets as a natural and integrated part of the curriculum, to solve creative problems receiving the feedback inherent in coding.
- Science: Spreadsheets are laboratories that enable us to experiment with quantitative models and treat math, in Lynn Steen’s immortal words, as a science, a Science of Patterns. Imagine math as a science with students drawing from a rich collection of varied problems, projects, and case studies, to perform an experiment, collect data, build models, test and iterate those models, and share their work with others.
Getting Started—Open Web Schools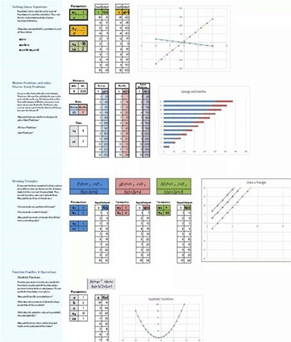
Trying something new in education today is just plain hard. The constraints of standardized tests, the overloaded curriculum, and the drive to ensure acceptance at all levels make it challenging for schools and teachers to significantly deviate from the expected norms. We are constantly told change in education is glacially slow and tedious, and are led to believe that it must be incremental. We are admonished to be scientific and to test every new thing we do, to see if it is better than the old even though we don’t test the old for its efficacy. What if math education is really a house of cards that one small change would bring down the whole? What if, for example, we slightly changed the instructions on standardized tests, allowing students to use the web to reference anything, to calculate anything, to interact with friends or even strangers for support? They will have these tools when they must solve real business problems, so should we not test them likewise? Surely, the tests will have to radically change, and the way we prepare students will require a revolution in curriculum and instruction, but the tools already exist and it is just a matter of implementing them for schools.
Schools must become places where every student has web access. Our job is to prepare students for the world they inherit, to make sure they learn to use the web properly and safely. An open-web school views the web as a great library, a repository of content, tools, and communications, where every student can find tools, things, and people of interest to them and needs to learn how to do this efficiently, safely, and honestly.
Curriculum and instruction will naturally fundamentally change. An open-web vision of schooling uses the internet as a repository of problem-solving lessons created by a variety of authors and even students, a case studies library with the variety and richness essential to engaging every student. It is replete with real-world data and technology so that kids find their school reflects their digital age. It is a place where students become teachers because they will have to explain how and why they solved a problem, and teachers become students because they will have to ask for such explanations. It is a fountain where creativity is not just valued, but flourishes. This vision, rich in collaboration and communication, creativity and critical thinking, is within our grasp. We need only open our schools to the web and make tests of student learning open-web as well to unleash a revolution driven not by a few but by many, not just in math but in all subjects, not just in one grade but in all grades. We need only imagine our students harnessing the power and tools of the web in collaboration with classmates to truly make their learning their own, and our schools to achieve the vision we share for 21st century learning where all kids thrive.
For more, see:
- ‘Why Do We Have to Learn This?’—Part I
- Podcast: Chad Dorsey on Modeling and Data Science in STEM Education
- Bad Bargain: Why We Still Ask Kids to Factor Polynomials and How We Fix It
Stay in-the-know with innovations in learning by signing up for the weekly Smart Update.
Art Bardige is the CEO of What If Math; whatifmath.org is open-web, with a growing collection of labs as exemplars accessible and free to all. Connect with him on Twitter: @artbardige.






0 Comments
Leave a Comment
Your email address will not be published. All fields are required.