‘Why Do We Have to Learn This?’ – Part I

By: Art Bardige

It is widely accepted that the math our students learn in school today has little to do with the math they will use in their jobs in our increasingly technology-driven society. Yet, we believe it is required and serves as a necessary and proper foundation. As a math educator and digital learning pioneer, I have long held these common views. But a chance discovery of the table of contents of a math book written by an obscure medieval mathematician revolutionized my thinking; overturning this conventional wisdom and enabling the reimagination of math education—indeed of all schooling for the 21st century.

The year 1200 was not auspicious, revolutionary, or defining. Thirty years earlier the foundation of the Leaning Tower of Pisa had been laid crowning Pisa as the dominant trading city in Europe. Just a year earlier Richard, King of England, died in France initiating his brother’s, Prince John, tumultuous and historic reign. And four years later the fourth Crusade overran Constantinople, marking the decline of the Byzantine Empire and the rise of the European city-states. 1200 was also the year Leonardo, a 30-year-old trader, returned to Pisa, the city of his birth, to write a math book for Pisan traders and merchants. Little could he have imagined that this work, “Liber abaci, The Book of Calculation”, published two years later, would define and dominate the mathematics students learn in school today 800 years later and impact 21st century life like no other relic of the Middle Ages.

Leonardo had sailed to Algeria as a young boy to join his ambassador father, who had him tutored in Arabic arithmetic and algebra, then academic subjects, unknown and unused in medieval business. Merchants used Roman math and calculated on an abacus. Sufficient for the Roman Empire which required conquered people to use its monetary and weights and measures systems, Leonardo saw it as an obsolete and burdensome technology in medieval times when every city-state was its own empire with its own weights, measures, and money-requiring business to solve ratio and proportion problems. Multiplication and division thus replaced addition and subtraction as the common operations, making the abacus an inefficient ineffective computation technology and Roman numerals a cumbersome symbol system.

Leonardo applied the math he had learned: Arabic symbols, place value, and the algebra of solving equations to develop standardized processes (algorithms) for calculation using paper. Paper, a relatively new technology in Europe, had been imported from China a century earlier for decoration. By Leonardo’s time it was a commodity produced in abundance by water-powered mills. In “Liber abaci,” Leonardo used paper to develop algorithms for solving the kinds of business problems he had encountered as a trader. His algorithms, the word a medieval corruption of al Khwarizmi’s name, would appear familiar to us today in function but not in form. History has treated Leonardo of Pisa, nicknamed Fibonacci in the 19th century, as a mathematician of minor import. I never expected to find in his biography anything of great mathematical or educational consequence. Little could I have imagined my utter shock and surprise when I turned to a page of this biography and saw the table of contents of “Liber abaci.” It was a near-exact replica of the scope and sequence of our K-12 math curriculum!

I cannot tell you whether it was my years as a math educator and author, my fascination with the ‘standard’ scope and sequence, my interest in the history of mathematics, or perhaps just some lucky insight, that led me to this discovery. For, Leonardo’s chapter titles were often obscure, sometimes not headings but the first words in the chapter. Of course, I followed that initial insight by studying the text in this first ‘textbook.’ Yes, for all intents and purposes, this was the math we expect all students to master from first grade to twelfth, from place value through solving quadratic equations. The math content designed and developed by Leonardo of Pisa for medieval business, “arithmetic necessary to merchants”  in the year 1202, remains the lessons we teach our kids today.

That math is not basic, foundational, or necessary—nor is it used in business. When was the last time you did long division, divided fractions by inverting and multiplying, or simplified a rational expression? Leonardo’s math is obsolete! Business no longer uses paper algorithms. We compute on screens mainly on spreadsheets. Our algorithms are computer algorithms. Our problems are no longer focused on solving equations; that is automatic, just ask Google. Today in business we use functions and build them into models to work with and analyze data. And even when we do not use spreadsheets as such, we use their format and their functional thinking. Yet, we rarely if ever encounter such problems in our schools. Our students do not learn to apply this digital technology, think functionally, build models or analyze real-world data, or use spreadsheets.

What would you subtract?

What if we, like Leonardo of Pisa in 1202, were to ask, “What math should our students learn to prepare them for business, for the work they will do?” A small group of us have been doing just that over the past five years. The answers prove to be fascinating. Paper algorithms that dominate math classrooms, that our kids spend a thousand or more classroom hours trying to master will never be used. Not just a few nasty algorithms like long division, but all of what students endlessly practice on paper worksheets. And in this age of digital technology, what makes even less sense is practicing paper algorithms on-screen ‘worksheets.’ Kids will never use computers that way. Nor will they ever add long columns of numbers on paper, regroup (borrow) to subtract, apply the traditional three-digit multiplication algorithm or any other paper algorithm for that matter, or add, subtract, multiply, or divide fractions on paper. Few, if any, will ever need to use the quadratic formula when their computer will solve any quadratic equation automatically.

But, you may ask, “Don’t students need to learn and practice these algorithms to understand the concepts?” Tell me, did memorizing the quadratic formula help you understand it? It is an algorithm, a process for finding solutions, far from transparent for most students, yet it marks the peak of learning algebra for the majority of them. Distinguishing algorithms from concepts is not easy. Just consider the widespread difficulty we have with ‘story’ problems. Students who may be facile in algorithmic practice, run into a brick wall when they have to solve word problems. Despite myriad methods originating with George Polya’s “How to Solve It” four steps to make such problems easier for students to solve, we’ve made little progress, continuing to frustrate students and teachers. We’ve made little progress because problem-solving is not a process; it does not succumb to an algorithm. It is conceptual. It requires an understanding of the concepts. Until we tackle that side of the equation, we cannot solve the problem it presents.

When we concentrate on repetitive paper algorithmic practice essential to calculation with Leonardo’s math, we lose sight of the concepts and students confuse algorithms with concepts. Long division and the three-digit multiplication algorithm become the concept of division and the concept of multiplication. We turn mechanical processes into conceptual ideas. They are not!

For example, picture the traditional long division algorithm: start by making a “guzinto” sign, put the divisor on the outside and the dividend inside, then guess how many times the divisor goes into the left digits of the dividend and put that number above the dividend, then multiply it by the divisor and put that below the dividend, then subtract, next bring down (yes, what kind of math operation is that?) the next dividend digit, and repeat the process until all of the digits are brought down and you are left with a remainder, whatever that new concept means.

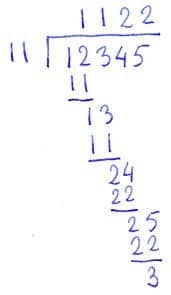
Tell me: “What does all of this mechanics have to do with the concept of division?” Nor is the old long division algorithm an anomaly, the new ones are a little less obscure but still do not represent the concept. Subtracting on paper (learned in second grade) requires students to master ‘borrowing’ now taught as ‘regrouping,’ neither of which is really about the concept of subtraction. No matter what we may call it, many students fail to grasp it, marking the beginning of a math failure ethic. The product of two three-digit numbers is a paper algorithm we usually think of when we picture multiplication, but few understand why it works. Kids don’t learn to visualize multiplication as a rectangle to understand the underlying concept because they and their teachers are focused on practicing the algorithm.

And even students who master whole number algorithms often sink in fifth grade when faced with fractions. Complex paper algorithms for adding fractions with unlike denominators or dividing fractions by inverting and multiplying offer little in the way of insight into their meaning or operations. Students not only get hung up on these operations, they’re so lost in their complexity that they never build an understanding of fractions. Based on the National Assessment of Educational Progress, half cannot order three fractions from smallest to largest in eighth grade! Why, when business today uses decimals to represent fractional quantities, do we still focus schooling on fractions?

Algebra is no better. By seventh and eighth grade, the mechanics of solving equations buries concepts. Students ask “What is x?”—locking them into thinking of math as calculation to be learned by mechanistic paper algorithmic memorization. And the results are painfully evident. More than a third of all college entrants fail math placement exams and are required to take non-credit remedial courses to prepare for college algebra.

To make matters worse, our focus on paper leads us to emphasize ‘handmath’ over ‘headmath.’ Handmath, calculating and solving problems on paper or keyboards, is algorithmic, following the patterns set by Leonardo. Headmath is mental, using concepts to simplify, estimate, and approximate solutions. Handmath relies on repetitive step-by-step processes that require fluency and careful sequencing. Headmath relies on understanding and number sense. While paper algorithm handmath is obsolete, headmath is not. I hear the complaint from the business community that students come to their jobs unable to judge quantities, tell whether a number they’re working with is a good value or not without turning on their calculator or opening up a spreadsheet. Today, it is more important than ever to practice headmath, for even in this realm of ubiquitous spreadsheet and calculator technology we rely on headmath and number sense to understand quantitative concepts, setup problems, build algorithms, and keep us on the right track. Our focus on paper algorithms and their standardized tests suck up classroom time, waste energy, and blind students to the critical headmath concepts. Removing paper algorithmic practice leaves us time to enable students to develop headmath proficiency.

For more, see:

• Podcast: Jo Boaler On the Limitless Mind and Learning Math That Matters
• Swap Algebra 2 for Data Science, Get a 1-Point Bump in GDP
• Bad Bargain: Why We Still Ask Kids to Factor Polynomials and How We Fix It

Stay in-the-know with innovations in learning by signing up for the weekly Smart Update.

Art Bardige is the CEO of What If Math; whatifmath.org is open-web, with a growing collection of labs as exemplars accessible and free to all. Connect with him on Twitter: @artbardige.