A Challenge to Bring Making Into Hour of Code

Hour of Code is upon us! This is such a fantastic event, and it has been lovely at my school to see students of all ages playing coding games, creating games in blocks-based programs like Scratch, and playing physical games that teach programming concepts like Robot Turtles. Hour of Code brings an international sense of unity in developing future programmers, and exposes students to coding who might otherwise not get that exposure.
And… we’re missing a great opportunity to offer kids experience with the deeper roots of computer science. If we want our students to begin to understand computer science that will lead them towards creating truly innovative and new scientific systems, they need to see more than color and blocks earlier on. They need to see the underlying mechanisms of computing: physics engines, not just graphics of video games; logic and calculations, not just beautiful data representations.
So, I offer this challenge: for Hour of Code, dig deeper below the surface of computer science. Further, I’ll even offer a specific activity to try out, even if you’re not a computer science expert:
Challenge your students to build a mechanical 4-bit Boolean adder, inventing their own physical logic gates. That might sound like a lot of insurmountable terminology, but it’s understandable. (P.S. I’m not a computer scientist!)
Boolean logic provides the simple rules and functions that form the foundation of modern computing. All of our programming languages – Fortran, C++, Python, Java, hundreds more – produce instructions that are broken down by the computer into simple Boolean logic operations. By creating a simple adder with only a few easy-to-understand rules, students can begin to develop a sense of how just a few basic rules can be scaled up to make those gorgeous video games or mobile phone operating systems.
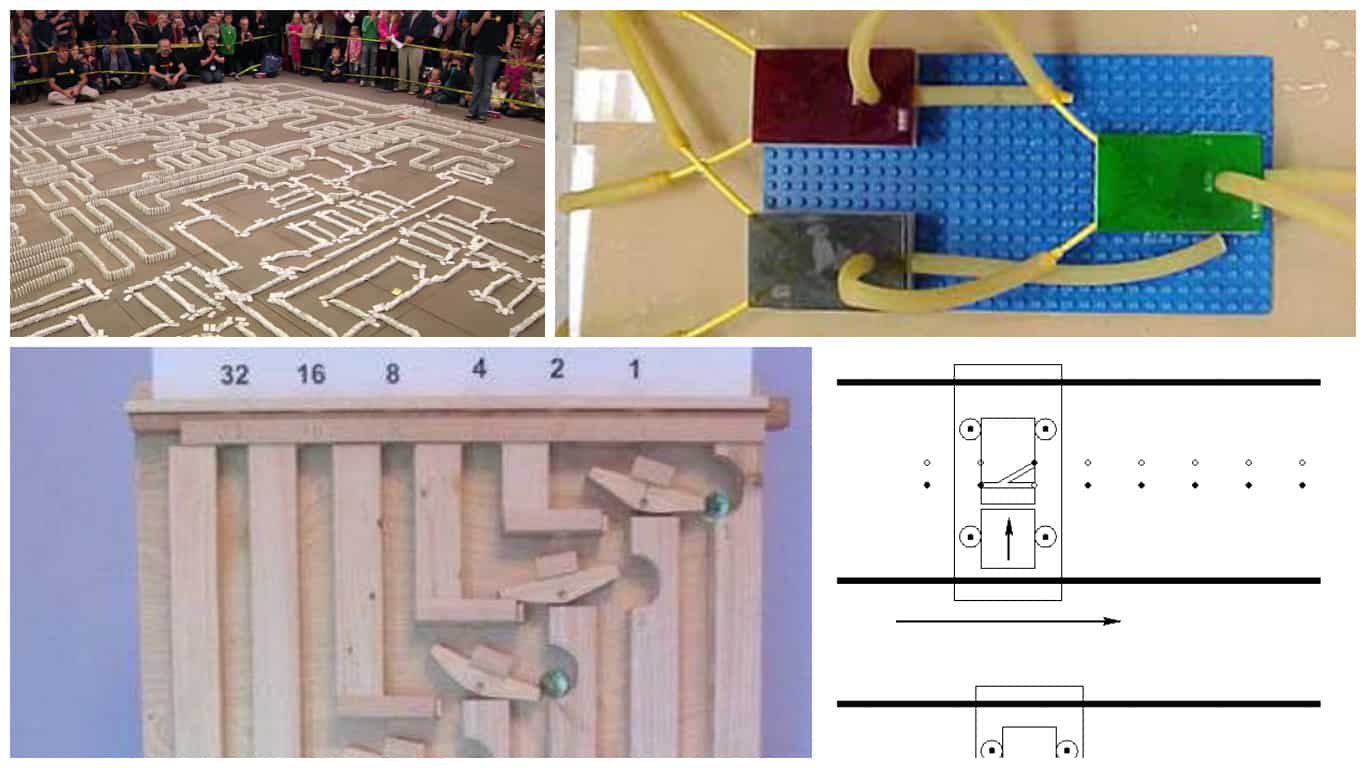
To teach this essence of programming – Boolean logic – you’ll also integrate math, a bit of history, and my favorite: “making.” Computer scientists of the future need to develop their mechanical sense, physical tinkering and prototyping ability, and persistence in working through problems. “Making” brings all of these to the fore. Several (but not many) makers who’ve come before us have created some clever physical representations of logic gates or even full Boolean adders, and many many more possibilities exist.
Invention credits, clockwise from top left: Matt Parker, Paolo Blickstein, Matthias Wandel, Greg Johnson
So, how are you – for example, 5th grade teacher with expertise in the humanities – going to challenge your kids to build a Boolean adder? I’m so glad you asked…
First and foremost, understand that Boolean addition is adding in “base 2.” Essentially, that means that place value is in multipliers of 2 instead of 10 — you carry to the next place every 2 counts instead of every 10. Instead of thousands place, hundreds place, tens place, and ones place you have 8’s place, 4’s place, 2’s place, and 1’s place. In the example below, the numbers in parentheses show the equivalents in base 10, which is the counting we’re used to. (That Boolean addition resource is really good… you should do the practice problems…)
Once you understand adding in “base 2,” then you understand how computers think. These are the 1’s and 0’s, or the “binary,” that you may have heard of. It’s easy for computers to think in binary, because they only have to keep track of 2 characters – an on state (1) or an off state (0).
The logic required to add in binary is much simpler than in “base 10” thanks to that reduction to only 2 states: At each place value, you can only either be adding 0+0, 1+0, 0+1, or 1+1. The trickiest trickiness comes when adding 1+1, since then you need to carry to the next place value. (Which, if you really are a 5th grade teacher, you know that carrying and place value can be tough for students… Here is thet math integration I promised!)
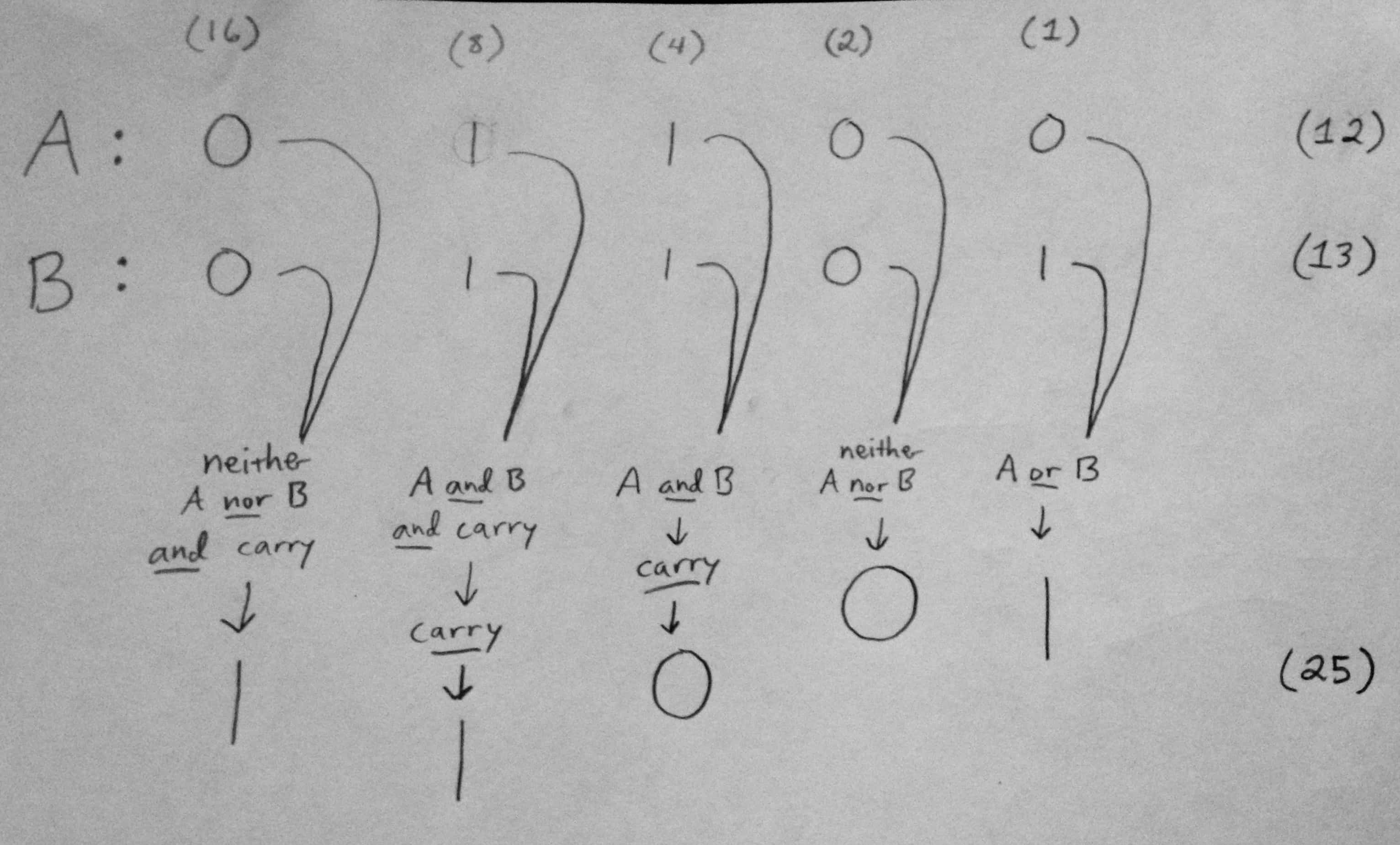
This is where, if you’ve ever heard about “logic gates” and AND, OR, or NOT, those concepts come into play. And they’re much simpler than all the new terminology might lead you to believe.
An AND gate simply says: if both of my inputs are “1” (or positive), then do ___[this]___
An OR gate says: if either of my inputs are “1”, then do ____[this]____
In the case of adding, inputs “1” OR “1” will result in an output of “1,” since 1+0=1. Inputs “1” AND “1” will result in “0” with a carry to the next place value. In base 2, 1+1=10. (A “1” in the 2’s place, and a “0” in the 1’s place.)
Applying AND and OR to our “base 2” addition looks like this example below:
An interesting bit of history here: those AND and other logic gates that did the Boolean adding for computers? In the early days of computing, the gates were vacuum tubes, which is a major reason that early computers were so large: vacuum tubes are huge! Vacuum tubes act as logic gates by either passing electrical current or not, depending on the electrical signals coming in, whereas your mechanical Boolean adder might pass marbles or drop dominos. An AND gate vacuum tube circuit will only send an electrical current output if it receives two electrical inputs. An OR gate vacuum tube circuit will send an electrical current output if it receives one of either electrical input.
The invention of the transistor – the next iteration of the computer logic gate – allowed us to start making smaller and smaller computers, and the development of semiconductors and integrated circuits let us pack billions of logic gates into a few cubic millimeters. Several Nobel Prizes have been awarded at points along this history.
Image credits: Williamson Labs, ComputerHistory.org/University of Manchester, ElectronicsByExample
So now that you understand how Boolean addition works, and its relevance to computing, how might you support your students in inventing their own version of a mechanical Boolean adder?
In each of the examples offered in the images, each rocker or switch or other physical gate represents the action of a single Boolean logic gate. Considering that our integrated circuits today contain billions of transistors – billions of logic gates – you can imagine how gigantic a smartphone made of physical gates would be! In the process of thinking through how to create gates themselves, students must develop a deep understanding of how computers use these simple building blocks to actually conduct these incredibly complex operations.
Here is where you just open up the possibilities and tinkering. Perhaps a student might want to work with a marble run and marbles to create their AND and OR gates? Perhaps a series of gears and pulleys would be best for another? Another might want to expand on Paolo Blickstein’s example in the image at the top, in which the user inputs water streams at each place value, and the solution to the addition problem comes from which water streams escape at the end. The critical bit is to create a device that allow you to input either a “1” or a “0” into however each place value (all of my written examples are 5-bit, or have 5 place values) for two numbers, and then the device returns an output that is the sum of those two numbers!
Invention credits: Yamamiya Takashi, Mechanical Logic, ThinkMaths.co.uk, Michael Littman, John Honniball. Also check out these final two awesome examples using flippers and marbles.
In devising these mechanical systems for what is now almost an exclusively digital function, your students can be retracing the steps of inventors of the earliest computers and computational algorithms: Charles Babbage (who designed the first mechanical computer), Ada Countess of Lovelace (who wrote the first computational algorithm), and even Joseph Marie Jacquard (who developed critical elements of the automatic loom – a precursor to Babbage’s mechanical computer).
(I highly recommend the graphic novel The Thrilling Adventures of Lovelace and Babbage by Sydney Padua as a language arts integration!)
Computer science isn’t all about digital programming and games. There’s critical underlying physics and logic that all of our programming languages ultimately get broken down into within the computer. And it’s not beyond comprehension – in fact, we teach alternate bases already, so this is just a great application of a math concept we already teach!
I challenge all of us to pull these critical computer science concepts up from the depths, and to incorporate physical “making” into our Hour of Code! I look forward to your reports, comment below.
For more blogs by Lindsey Own, check out:
- 3 Lenses for Developing Deeper Driving Questions
- 8 Tips in Taking on School-Wide Makerspace Leadership
- Houston, Texas | A Growing Center for DIY Innovation
Stay in-the-know with all things EdTech and innovations in learning by signing up to receive the weekly Smart Update




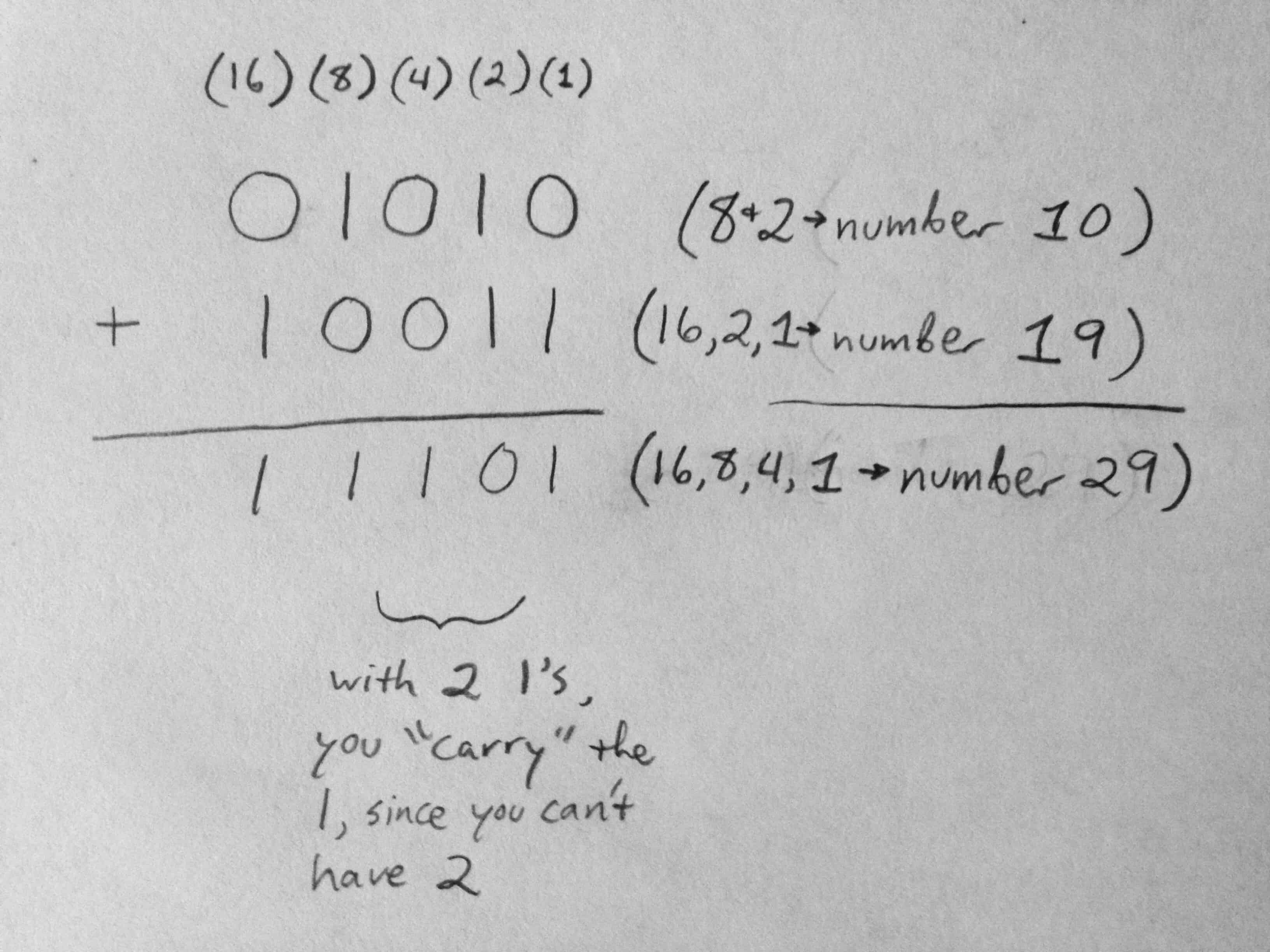





0 Comments
Leave a Comment
Your email address will not be published. All fields are required.